PDF) Quarternions and the Four Square Theorem
Por um escritor misterioso
Last updated 13 junho 2024

The Four Square Theorem was proved by Lagrange in 1770: ev- ery positive integer is the sum of at most four squares of positive integers, i.e. n = A2 +B2 +C2 +D2;A;B;C;D 2 Z An interesting proof is presented here based on Hurwitz integers, a subset

Commutative quaternion algebra and DSP fundamental properties: Quaternion convolution and Fourier transform - ScienceDirect

LAGRANGE'S FOUR SQUARE THEOREM Theorems, Lagrange theorem, Number theory

The Real and Complex Hermitian Solutions to a System of Quaternion Matrix Equations with Applications – topic of research paper in Mathematics. Download scholarly article PDF and read for free on CyberLeninka

Mathfest 2018 Puzzles: Quaternion Groupdoku

Algebra paper retracted because of questions about the “integrity of the mathematics” – Retraction Watch

PDF) Quarternions and the Four Square Theorem

Solving Sums of Squares in Global Fields Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation

Quaternions in Signal and Image Processing

Symmetry, Free Full-Text
Topics in Quaternion Linear Algebra
On the Continuity of the Generalized Inverse

PDF) Quarternions and the Four Square Theorem

PDF) Quarternions and the Four Square Theorem

Quaternions in mathematical physics (1): Alphabetical bibliography – arXiv Vanity
Recomendado para você
-
 PDF) Lagrange's Four-Square Theorem13 junho 2024
PDF) Lagrange's Four-Square Theorem13 junho 2024 -
 Lagrange's four-square theorem13 junho 2024
Lagrange's four-square theorem13 junho 2024 -
Jacobi's four-square theorem - Wikipedia13 junho 2024
-
 What's so interesting about squared numbers? Lagrange's Four Square Theorem13 junho 2024
What's so interesting about squared numbers? Lagrange's Four Square Theorem13 junho 2024 -
 Solved QUADRA range's Four-Square Theorem) If n is a natural13 junho 2024
Solved QUADRA range's Four-Square Theorem) If n is a natural13 junho 2024 -
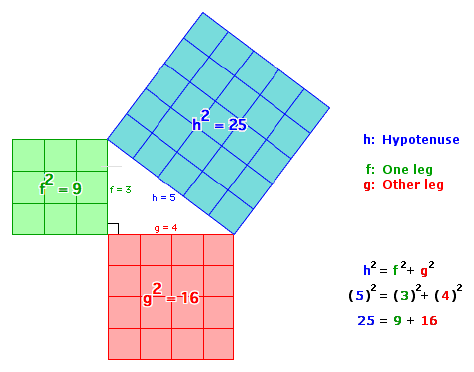 Pythagorean Theorem13 junho 2024
Pythagorean Theorem13 junho 2024 -
Lagrange's three square theorem13 junho 2024
-
 Lagrange's Four-Square Theorem by Julian TSE13 junho 2024
Lagrange's Four-Square Theorem by Julian TSE13 junho 2024 -
Stable/Patient Sort: Bit-Manipulation-To-Solve-Problems-Easily-And-Efficiently, PDF, Square Root13 junho 2024
-
 Answered: The Modular Operation r mod m = r…13 junho 2024
Answered: The Modular Operation r mod m = r…13 junho 2024
você pode gostar
-
 Naruto: Minato Namikaze, o Quarto Hokage, ganhará um mangá one-shot13 junho 2024
Naruto: Minato Namikaze, o Quarto Hokage, ganhará um mangá one-shot13 junho 2024 -
 Roblox Corporation - Gematsu13 junho 2024
Roblox Corporation - Gematsu13 junho 2024 -
 Mario Strikers: Battle League - US Version13 junho 2024
Mario Strikers: Battle League - US Version13 junho 2024 -
 Battlefield 2042 Devs Say It's A Really Good Game Now - Insider Gaming13 junho 2024
Battlefield 2042 Devs Say It's A Really Good Game Now - Insider Gaming13 junho 2024 -
 Fandom Gaming on X: Download the Official Terraria Wiki App from Google Play, iTunes / X13 junho 2024
Fandom Gaming on X: Download the Official Terraria Wiki App from Google Play, iTunes / X13 junho 2024 -
 Vampire: The Masquerade - Bloodlines 2 - Xbox One First Blood Edition : Plaion Inc: Everything Else13 junho 2024
Vampire: The Masquerade - Bloodlines 2 - Xbox One First Blood Edition : Plaion Inc: Everything Else13 junho 2024 -
 Stream ULTRA BEASTS! music Listen to songs, albums, playlists13 junho 2024
Stream ULTRA BEASTS! music Listen to songs, albums, playlists13 junho 2024 -
/pic57994.jpg) Blood Feud in New York, Board Game13 junho 2024
Blood Feud in New York, Board Game13 junho 2024 -
how to get advanced raids blox fruit|TikTok Search13 junho 2024
-
 Yumeko Jabami Workout: Train to Become Kakegurui's Protagonist!13 junho 2024
Yumeko Jabami Workout: Train to Become Kakegurui's Protagonist!13 junho 2024


